「数論幾何の難しいところは置いておいて面白い話が知りたい」、「数論幾何における考え方のエッセンスみたいのが知りたい」
こういった疑問にお答えします。
数論幾何は、数学の中の一分野で、幾何学的な手法を用いて数論の問題に取り組む学問です。
数論幾何は、前提となる数学的知識が多く難解な分野として有名です。そんな数論幾何における重要な考え方に「モチーフの理論」があります。
今回は、モチーフについて初心者でも雰囲気がわかるようにご紹介します。
そもそも数論幾何ってなに?って方はこちらの記事からどうぞ→【入門】数学で一番難しい分野?!「数論幾何」ってどんな学問かを紹介してみた
(※この記事では、数学的な厳密さを保証せずに、モチーフの雰囲気を伝えることを目的とします。悪しからず。)
抽象化の考え方

数論幾何に限らず、数学の研究では多くの場面で「抽象化」あるいは、「一般化」という考え方がキーワードになります。
例えば、「Aという問題が〇〇という方法で解くことができた。また、BというAとは異なった問題が同じ〇〇という方法で解けた」とします。
この時、ひょっとしたらAとBは表面的には全く違うものに見えるけど、実は“本質的には”同じ問題なのではないか?と考えることができます。
すると、「AとBに共通する性質は何だろう?」、「〇〇の方法の何が本質的に効いて問題が解決しているのだろう?」と思考を進めることができます。
このようなプロセスを数学では「一般化」、「抽象化」と言います。
一言で言ってしまうと、数論幾何(数学)では、異なる問題どうしから共通する性質を抜き出して、一般化した問題を考えることが大事だということになります。
セザンヌの「モチーフ」の考え

ここで少しだけ数学から話を離れます。
19世紀のフランスの画家ポール・セザンヌは、「近代絵画の父」と呼ばれており、従来の伝統的な絵画のルールにとらわれない独自の絵画様式を探求した人物です。
ポスト印象派の画家として、後々のキュビスムをはじめとする20世紀の美術に多大な影響を与えました。
セザンヌは自身の絵画評で、従来のうつろい行く光と影で描写する印象派から離れ、実際の絵画対象(=モチーフ)を確実に捉えるという独自の絵画様式の確立に尽力しました。
彼は、事物の表面的な部分ではなく、そのモチーフを確実捉えることに重きを置いていくことで本質に迫ろうとした画家と言えます。
数論幾何の「モチーフ」の考え

一方、数論幾何では、抽象化によって得られる幾何学的対象を「モチーフ」と呼びます。
これは、数論幾何を創始した数学者アレクサンドロ・グロタンディークが、上で紹介したセザンヌのモチーフの絵画評(=対象の表面的な部分ではなく本質に着目する)に発想を得て導入した用語です。
数論幾何におけるモチーフには数学的な定義存在しますが、ここで紹介するのは余白が狭すぎるため控えます。
定義に触れずに、もう少しだけ数学的な意味合いでのモチーフを紹介します。
そのために一つだけ「コホモロジー」という用語導入します。
※以下は少し難しい内容になります。
コホモロジーとは?
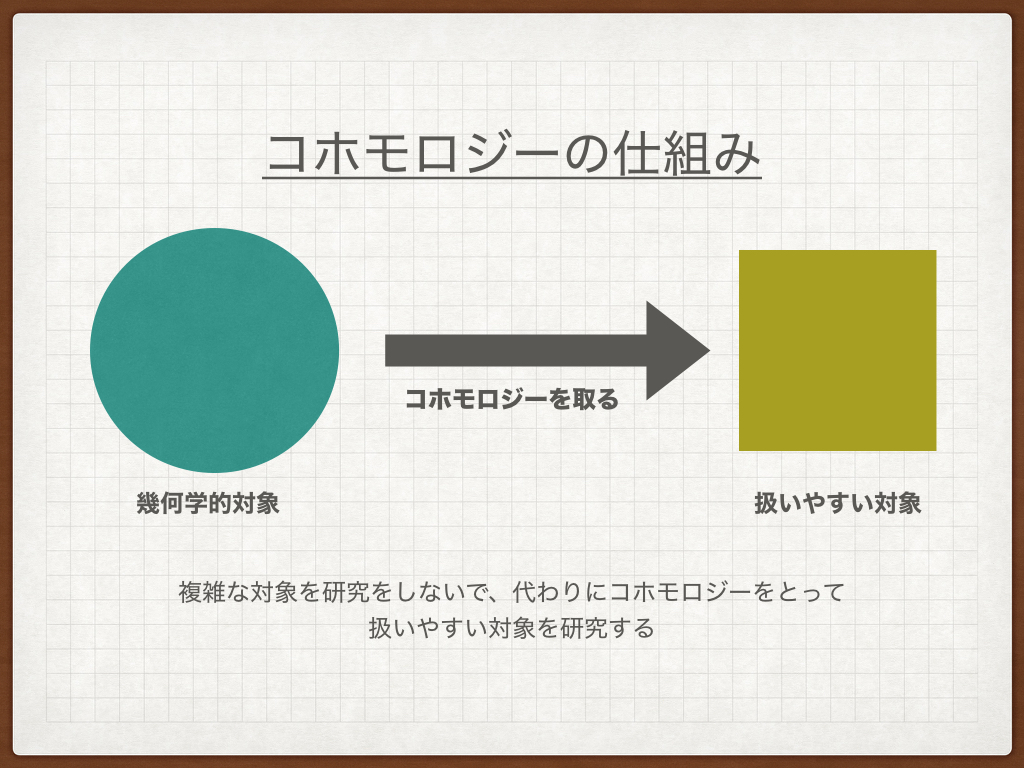
コホモロジーとは、大雑把に言ってしまえば幾何学的対象を調べる”道具”で、複雑に思える幾何学的対象から、扱いがよくわかるものとしてのそのエッセンスを取り出す働きをします。
多くの場合、この幾何学的対象は「代数多様体」と呼ばれるもので、この代数多様体からコホモロジーを構成することができます。
コホモロジーは、元の代数多様体の性質(=エッセンス)を引き継いでいることが多く、しかも線型空間(=足し算、引き算、掛け算ができる空間)として扱えるため数論幾何の研究では重要な研究対象になります。
実はこのコホモロジーには、たくさんの種類があって調べたい代数多様体の種類によって使い分けています。
種々のコホモロジー
ベッチコホモロジー
ド・ラームコホモロジー
エタールコホモロジー
クリスタリンコホモロジー などなど
これらのコホモロジーは別々に構成されたもので、当初は互いに独立したものでした。
ところが、これらのコホモロジーの研究が進むにつれて、ある条件ではコホモロジーが一致する(=同じものと考えることができる)ということが次第にわかってきたのです。
例えば、ある条件を満たす代数多様体に対して、そのベッチコホモロジーとド・ラームコホモロジーが一致するといった具合にです。
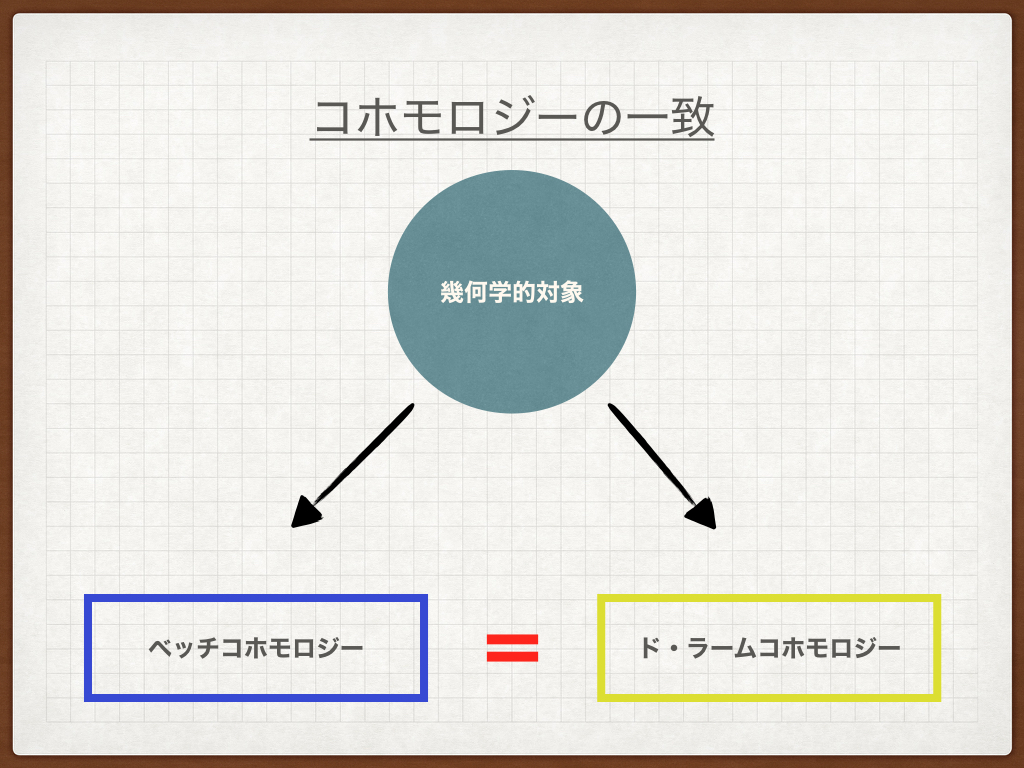
このようなコホモロジーの一致は、その他のコホモロジーでも見られており、これを受けて先のグロタンディークは、「これらのコホモロジー理論を統一するもっと本質的な存在があるはずだ」と考えました。
その”本質的な存在”こそが上で紹介した「モチーフ」と呼ばれるものです。
まとめ

画家セザンヌが提唱した「モチーフ」の考えは、その後、数論幾何における「モチーフの理論」を生み出すきっかけになりました。
セザンヌの「モチーフ」も数論幾何の「モチーフ」もどちらも物事の「本質は何か?」を追求する取り組みと言えるでしょう。
この考えは、数論幾何に限らず、広く社会でも通用する姿勢ではないかと個人的には思います。
今回は、だいぶ専門的な話題になってしまいましたが、少しでも「モチーフ」の雰囲気が伝われば幸いです。












