数論幾何(スウロンキカ)? なにそれ、美味しいの?
って人の為に「数論幾何」を大学院で研究していた僕がどんな学問かを紹介します。
(※この記事では、数学的な厳密さを保証せずに、雰囲気を伝えることを目的とします。悪しからず。)
そもそも数論幾何とは?

数論幾何(ちゃんと言うなら数論幾何学)は数学の中の一分野で、整数に関する様々な問題を幾何学的な手法を使って研究する学問です。
「整数」というのは、
$$\mathbb{Z}=\{\dots,-5,-4,-3,-2,-1,0,1,2,3,4,5,\dots\}$$
のことで、0とそれに1ずつ足していって得られる数と1ずつ引いていって得られる数全体の集合のことです。
この整数に絡む問題を研究する分野は個別に「整数論」と呼ばれています。
なので、数論幾何をもう少しカッコよく説明すると、整数論の問題に対して、幾何学的なアプローチを使って研究をする学問と言えます。
幾何学的なアプローチとは?
まずは、どう「数」と「図形」が結びつくかの雰囲気を説明します。
例えば、「三角形」を思い浮かべてみると、図形としては単に「三角形」(下図参照)ですが、

その図形の中には、頂点の数や辺の数、面積、角度のような数字を紐づけることができます。
例えば、下の表みたいな感じです。
| 項目 | 三角形 | 四角形 |
|---|---|---|
| 頂点の数 | 3 | 4 |
| 辺の数 | 3 | 4 |
| 面積 | 底辺の長さ×高さ÷2で求められる数 | 縦の長さ×横の長さ×高さで求められる数 |
この辺りは小学校でもやったようなことですが、改めて数と図形を”結びつけている”という視点を持ってみると、確かに図形⇆数の対応を考えられそうな気がしてきます。
もう少しだけ難しいものを考えてみると、高校で習った円の方程式を思い出します。
$$x^2+y^2=1$$
というやつです。この式がなぜ円だったかというと、この式を満たすxとyを座標平面上にポツポツと描いていくと最終的には円になるということでした。
では、そのようなxとyはどうやったら見つけることができるかと考えてみます。
少し計算するとわかりますが、
$$(x,y)=(1,0),(0,1),(-1,0),(0,-1)$$
はこの式を満たします(ちょうど、円がx軸、y軸と交わっている点です)。
そこで、例えば(-1,0)を通る直線を考えるとこの直線は円ともう一点Aで交わるのがわかります。
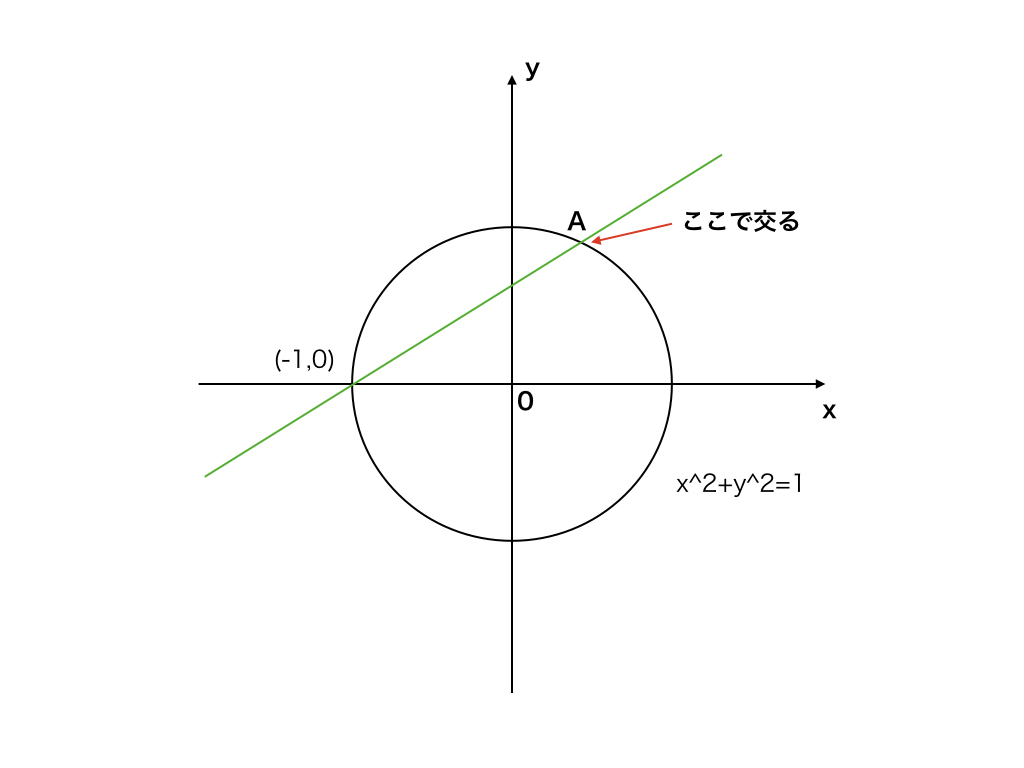
この直線の傾きを考えると、傾きが有理数(※)になるようなものを考えれば自然とAは有理数になります。
(※有理数とは、二つの整数a,bを用いてa/bのように分数の形で表すことができる数のこと。任意の整数は、b=1として有理数として考えらることができる。)
つまり、円の方程式の有理数解は、傾きが有理数の直線と1対1に対応していることがわかります。
$$\{\mbox{方程式の有理数解}\}\longleftrightarrow \{(-1,0)\mbox{を通る傾きが有理数の直線}\}$$
このような感じで、どことなく図形を使うと視覚的に数の問題(=今回だったら円の方程式)をスッキリと解くことができる(できそう)な雰囲気が伝わったかと思います。
実は、ここで紹介した直線と有理数解の考え方は、あの有名な「フェルマーの最終定理」の証明にも応用されるとても優秀な考え方なんです。
「フェルマーの最終定理」の証明については、ここでは触れませんが気になった方は以下の本とかで勉強してみるといいでしょう。
フェルマーの最終定理が気になった方へのおすすめ本
フェルマーの最終定理の解決までの物語を知りたい人はコチラがおすすめ
フェルマーの最終定理の証明をある程度数学的な側面も理解してみたい人はコチラがおすすめ
数論幾何は難しい?

数論幾何はよく、数学の中でも一番難しい分野、天才(奇人?)がやる分野などと言われます。
実際、何を持って「一番」難しいかは人それぞれだと思うので、一概には言えませんが、それでも難解な分野であることは事実です。
数論幾何が難しい理由
数論幾何が難しいと言われるには、以下のような理由があります。
前提となる知識が膨大
数論幾何を研究するためには、代数幾何、整数論、位相幾何、関数論、などなど様々な数学の分野に関する知識が必要です。
特に、代数幾何は非常に難解な分野でこの分野を勉強している段階で挫折してしますことが多いです。
数論幾何は、代数幾何の道具立(=様々な理論や定理)をフルに活用して、整数論の問題にアプローチをするため、代数幾何の知識は必須となります。
そもそも整数論が難しい
これを言ってしまうと元も子もなくなってしまいますが、数論幾何が相手にしている整数論自体が非常に難解な分野です。
その難解な整数論の問題に対して、難解な代数幾何を使って研究をするので、結果として数論幾何は難しいということになります。
数論幾何研究者は天才が多い?
数論幾何の分野には天才が多いと言われています。その証拠に、数学界のノーベル賞と呼ばれる「フィールズ賞」受賞者には数論幾何の研究者が多いです。
ここでは、数論幾何の分野で有名な数学者を少しご紹介します。
アレクサンドル・グロタンディーク(Alexander Grothendieck)

ドイツ出身のユダヤ系フランス人の数学者です。代数幾何の分野で「スキーム」という理論を創設し、スキーム理論を用いて数論幾何の問題を多く解決しました。
実際、「数論幾何」という用語を創出したのもこのグロタンディークです。
現在の数論幾何で重要な様々な理論の多くを作り出し、代数幾何、数論幾何の分野で多大な貢献をした数学界の巨人です。
ピエール・ドリーニュ(Pierre Deligne)

グロタンディークの弟子で、ベルギーの数学者です。グロタンディークが作り出した当時の最新鋭の数論幾何的理論を発展、用いることで「ヴェイユ予想」と呼ばれる大予想を解決しました。
23歳でIHÉS(=フランスの数学研究所)の客員教授、26歳でIHÉS教授、34歳のときフィールズ賞を受賞した天才です。
彼はヴェイユ予想の解決だけでなく、その後も「ザリスキ予想」、「ラマヌジャン予想」、「ヒルベルトの第21問題」など多数の超難問を解決するなどの業績を残しています。
ゲルト・ファルティングス(Gerd Faltings)

By: owpdb.mfo.de
ドイツ人数学者で、現在の数論幾何で中心的な理論である「p進Hodge理論」を構築した人物です。
「モーデル予想」と呼ばれる有理数体上の曲線に関する予想の解決をしてフィールズ賞を受賞しています。
そのほか、「ファルティングスの定理」や「概純粋性定理」など多くの重要な発見をし数論幾何の分野に大きな影響を及ぼしています。
その他、J.P.セールやマキシム・コンツェビッチ、日本の望月新一など数論幾何には多くの天才がいます。
数論幾何は世の中の役に立つか?

数論幾何は世の中の役に立つか?
これに対する答えは、数論幾何に限らず(純粋)数学全般に言えることかもしれませんが、実生活で普通の人が感じられるレベルではNOではないでしょうか。
ただし、数学は様々な技術の根幹であることを考えると知らず知らずのうちにその恩恵を受けているという風には言えるかもしれません。
例えば、数論幾何で言えば、数論幾何で重要な研究対象である「楕円曲線」と呼ばれる対象は、世の中の様々な暗号技術の基本を与えているものになります。
最近流行りの仮想通貨(及び、ブロックチェーン技術)でも、その高いセキュリティ性はこの暗号技術を応用することで実現しています。
数論幾何の参考書
ここまで、とってもざっくり「数論幾何とはどんな分野か?」について、その雰囲気をご紹介しました。
少しでも興味が湧いて勉強したいなと思った方のために、最後におすすめの参考書をご紹介します。
数論幾何の教科書
数論幾何をズバリ解説している教科書はなかなかありませんが、まずはもう少し数学的な内容に触れつつ勉強をしてみたいという方には以下の本がおすすめです。
初等整数論 ―数論幾何への誘い―
数論幾何についての最新の研究のエッセンスを知りたい方はこちらがおすすめです。
数学の現在 i
本格的に勉強をしてみたいという方には、まずは数論幾何のツールである代数幾何を勉強する必要があるので、標準的な教科書である以下がおすすめです。
Algebraic Geometry (Graduate Texts in Mathematics. 52)
スキーム論については、以下の本もおすすめです。
Algebraic Geometry And Arithmetic Curves (Oxford Graduate Texts in Mathematics)
まとめ

数論幾何は数学の最先端の分野です。非常に難解な分、理解できたときの喜びも大きいです。
数と図形という小学校以来親しんできた対象を究極まで突き詰めると数論幾何の理論に行き着きます。
ぜひ、挑戦してみようと思った方は勉強を始めてみてはいかがでしょうか?












