数学の勉強を進めていると「多様体」という概念に出会います。
英語では、「manifold」と呼ばれるもので、平面や曲面などの空間を一般化した現代数学の基礎的な概念の一つです。
※代数幾何などで扱う「多様体(variety)」もありますが、その話はまた今度。
今回はそんな多様体について、一体どんなものかということをしっかりとした基礎を元に理解をしたい方におすすめできる教科書をご紹介します。
今回ご紹介する教科書は、松本幸夫著『多様体の基礎』(東京大学出版会)です。
東大出版の数学教科書シリーズはレベルの高いものも多く、とっつきにくいイメージもありますが、この『多様体の基礎』はとてもわかりやすく、敷居も高くない初学者におすすめの教科書です。
多様体とは?
書籍の紹介の前に、ここでも簡単に多様体について説明しておきましょう。
多様体とは、冒頭にも触れたように平面や曲面を一般化した空間概念です。
小学校以来、平面や曲面は算数や数学でも登場して馴染みのある方も多いはず。平面をマス目に区切って(=x座標とy座標を入れて)、点(座標)を入れていくことで平面上の直線の式や平面の方程式を求めたりしました。
こんな感じのことを、曲面やもっと一般化してn次元の空間でやりたいと思った時に出てくるのが多様体です。
“多様”体という名前の通りグニャグニャと色々な形の図形を扱う分野になります(下の図参照)。
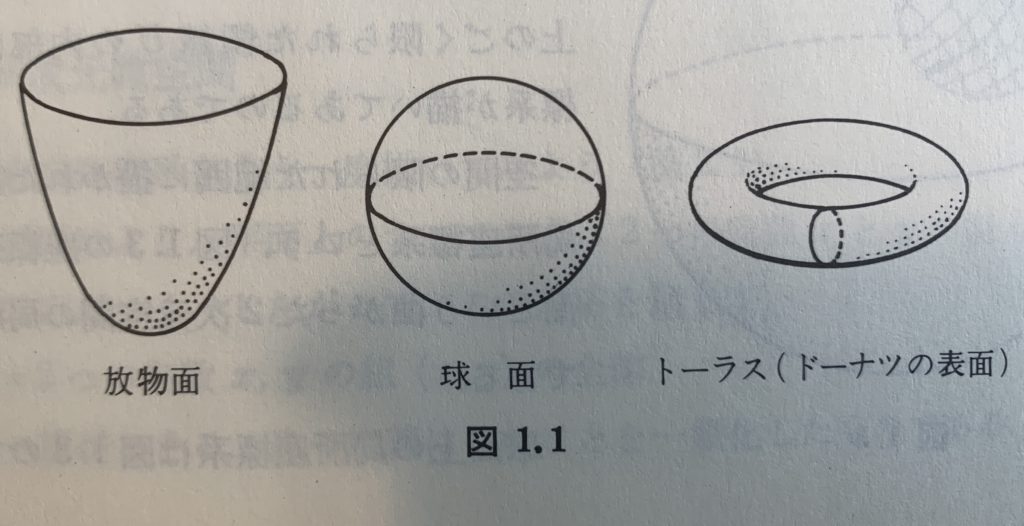
※『多様体の基礎』より。
そんな多様体について、大学初年度レベルの微分積分と線形代数(あと少しだけ位相)の知識を前提に、多様体のごく基礎的なところから解説したのが『多様体の基礎』になります。
『多様体の基礎』=ラノベ?!
『多様体の基礎』はその見た目からは想像できないほど初歩的なレベルから解説されており、数学の教科書にありがちな「行間が空きすぎてて理解ができない!」といったことが最初から最後まで無い、非常に初学者に優しいい教科書に仕上がっています。
そのため、数学徒の一部界隈では「ラノベ(ライトノベル)」とまで呼ばれており、認知度も高い人気の教科書です。
『多様体の基礎』のおすすめポイント
①行間が狭い
数学の教科書の多くは、紙数の関係で証明を省略していたり、証明が書いてあっても概略のみだったりすることが多いですが、本書は重要な定理の証明においてはしっかりと計算も示されており、証明を追うのが用意です。
また、証明の助けとなるイメージ図などもあり証明を理解しやすいです。
②盛り沢山すぎない内容
本書は、「この厚さから想像されるほど盛りだくさんの内容を含んでいない」と、まえがきにもあるように初学者に向けて必要最低限の多様体の基本的事項の紹介に留めており、あれもこれもと言った欲張った印象がなく安心して勉強できます。
より専門的な内容はあえて捨てることで、初学者向けの解説に紙数を割いた構成になっています。
③松本先生の人柄がわかる解説と証明
数学の教科書には著者の人柄がよく現れますが、本書もまさにそういった印象を受けます。
説明文や証明の構成からも、長年、東京大学、学習院大学で教鞭を取られてきた松本先生の勘所を抑えた非常に明快な、それでいて初学者に寄り添うような文章になっています。
著者の松本幸夫先生について

By: gakushuin.ac.jp
松本先生は、東大で学位取得後、東大や学習院大学で数学の教鞭を執られて、現在は学習院大学の教授を退官後、研究員として現在も精力的に研究をされている方です。
専門はトポロジー、特に4次元多様体です。
僕自身、学部は学習院の数学科出身で松本先生から直接、多様体の授業を受けました。非常に明快な説明と温厚な人柄に見え隠れするトポロジーへの情熱が印象的な先生でした。
実際、学部時代の数学で一番面白かった授業は松本先生の多様体論でした。
『多様体の基礎』はそんな松本先生の授業のエッセンスがたっぷり詰まった良書であることは、リアル授業を受けていた僕が保証します。
『多様体の基礎』が気になった方へ
ここまでで、少しでも多様体について「しっかりと勉強してみたい」「なんだか松本先生の雰囲気がどんなのか気になる」とか思った方はぜひ、手に取ってみてください。
多様体の基礎

By: amazon.co.jp
初学者向けに、学部1,2年レベルの微積分と線形代数、位相の知識を仮定して懇切丁寧に多様体に関する基礎的な事項を解説して多様体入門の名著。
多様体からもう少し進んだ内容も勉強してみたいという方に、同じく松本先生の著書から以下の2冊もおすすめです。
モース理論の基礎

By: amazon.co.jp
微分トポロジーの一理論であるモース理論(多様体の変形や分解を扱う理論)について書かれた教科書です。和書でモース理論について書かれた書籍は少ないですが、本書はその中でも一番わかりやすい本だと思います。
『多様体の基礎』同様、松本先生のわかりやすい解説のおかげで難解な理論もイメージを持って理解することができます。
多様体論を終えた後、多様体が活躍する理論を勉強してみたいと思われる方におすすめの教科書です。
新版 4次元のトポロジー

By: amazon.co.jp
松本先生のご専門である4次元多様体について書かれた教科書です。
低次元トポロジーの魅力がこれでもかと詰まった、正真正銘の名著だと思います。僕自身、旧版の方で基本群やロホリンの定理などこの本を使って勉強をしましたが、今回の新版では、ペレルマンによる3次元のポアンカレ予想を解決したことを節目に「30年を経て」が付記されており、松本先生の研究の視点なども織り交ぜながら最新の低次元トポロジーについて触れることができます。
高次元でのポアンカレ予想解決(スメール)、4次元での解決(キャッソン)、3次元での解決(ペレルマン)と時代とともにトポロジーがどのように移り変わり、重要な手法が誕生し、問題が解決されていったかが専門家の視点で勉強することができ、読み物としても優れた内容になっています。










